Symmetric relation
| Transitive binary relations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All definitions tacitly require the homogeneous relation be transitive: for all if and then |
A symmetric relation is a type of binary relation. Formally, a binary relation R over a set X is symmetric if:[1]
where the notation aRb means that (a, b) ∈ R.
An example is the relation "is equal to", because if a = b is true then b = a is also true. If RT represents the converse of R, then R is symmetric if and only if R = RT.[2]
Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation.[1]
Examples
[edit]In mathematics
[edit]- "is equal to" (equality) (whereas "is less than" is not symmetric)
- "is comparable to", for elements of a partially ordered set
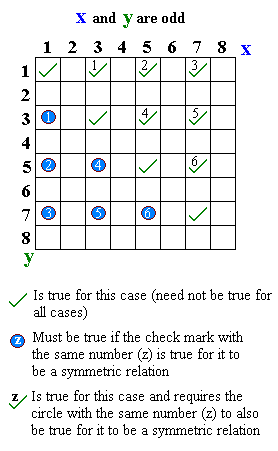
- "... and ... are odd":
Outside mathematics
[edit]- "is married to" (in most legal systems)
- "is a fully biological sibling of"
- "is a homophone of"
- "is a co-worker of"
- "is a teammate of"
Relationship to asymmetric and antisymmetric relations
[edit]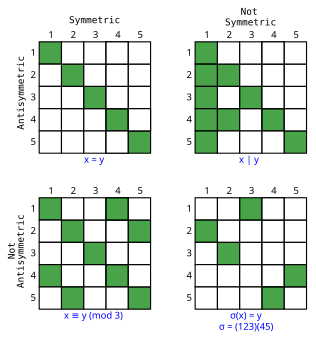
By definition, a nonempty relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").
Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.
| Symmetric | Not symmetric | |
| Antisymmetric | equality | divides, less than or equal to |
| Not antisymmetric | congruence in modular arithmetic | // (integer division), most nontrivial permutations |
| Symmetric | Not symmetric | |
| Antisymmetric | is the same person as, and is married | is the plural of |
| Not antisymmetric | is a full biological sibling of | preys on |
Properties
[edit]- A symmetric and transitive relation is always quasireflexive.[a]
- One way to count the symmetric relations on n elements, that in their binary matrix representation the upper right triangle determines the relation fully, and it can be arbitrary given, thus there are as many symmetric relations as n × n binary upper triangle matrices, 2n(n+1)/2.[3]
| Elements | Any | Transitive | Reflexive | Symmetric | Preorder | Partial order | Total preorder | Total order | Equivalence relation |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 1,024 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n(n−1) | 2n(n+1)/2 | ∑n k=0 k!S(n, k) |
n! | ∑n k=0 S(n, k) | |||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
Note that S(n, k) refers to Stirling numbers of the second kind.
Notes
[edit]- ^ If xRy, the yRx by symmetry, hence xRx by transitivity. The proof of xRy ⇒ yRy is similar.
References
[edit]- ^ a b Biggs, Norman L. (2002). Discrete Mathematics. Oxford University Press. p. 57. ISBN 978-0-19-871369-2.
- ^ "MAD3105 1.2". Florida State University Department of Mathematics. Florida State University. Retrieved 30 March 2024.
- ^ Sloane, N. J. A. (ed.). "Sequence A006125". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
See also
[edit]- Commutative property – Property of some mathematical operations
- Symmetry in mathematics
- Symmetry – Mathematical invariance under transformations